Earthquake duration magnitude
| Part of a series on earthquakes |
|---|
| Types |
| Foreshock • Aftershock • Blind thrust Doublet • Interplate • Intraplate Megathrust • Remotely triggered • Slow Submarine • Supershear Tsunami • Earthquake swarm |
| Causes |
| Fault movement • Volcanism • Induced seismicity |
| Characteristics |
| Epicenter • Hypocenter • Shadow zone Seismic wave • P-wave • S-wave |
| Measurement |
| Mercalli scale • Richter scale Moment scale • Surface wave magnitude scale Body wave magnitude scale • Seismometer Earthquake duration magnitude |
| Prediction |
| Coordinating Committee for Earthquake Prediction Earthquake sensitive |
| Other |
| Shear wave splitting • Adams–Williamson equation Flinn-Engdahl regions • Earthquake engineering Seismite • Seismology |
The concept of Earthquake Duration Magnitude - originally proposed by Bisztricsany[1] in 1958 using surface waves only - is based on the realization that on a recorded earthquake seismogram the total length of the seismic wavetrain - sometimes referred to as the CODA - reflects its size. Thus larger earthquakes give longer seismograms [as well as stronger seismic waves] than small ones. The seismic wave interval measured on the time axis of an earthquake record - starting with the first seismic wave onset until the wavetrain amplitude diminishes to at least 10% of its maximum recorded value - is referred to as "earthquake duration". It is this concept that Bisztricsany first used to develop his Earthquake Duration Magnitude Scale employing surface wave durations.
Contents |
Earthquake Duration Magnitude [Md] Development
In 1965, Solovev[2] proposed the use of total duration instead of the duration of surface waves. In 1972, Lee et al.[3] used coda duration for the first time to estimate Richter magnitude of local Californian earthquakes. Based on their study, they suggested that it is appropriate to estimate the magnitude of local earthquakes using signal duration. More recently, the development in instrumentation led to the use of signal duration to estimate the coda magnitude (Md) for earthquakes recorded on short-period vertical seismographs. Numerous studies determined the relation between coda duration and magnitude for different regions of the World. According to a recent study by Mandal et al. (2004)[4] previous studies showed that duration magnitude estimation is quite stable for local earthquakes ranging from magnitude Md 0.0 to 5.0.
Md Empirical Relationships
In two most recent investigations using statistically stable samples for Italian earthquakes [approximately 100,000 events over the period 1981-2002 in the Richter local [ML] magnitude range of 3.5-5.8] [5] and for Indian earthquakes examplified by an aftershock sequence of 121 events with Ms (surface wave magnitude) > 4.0 in 2001 in the Bhuj area of northwestern India [6], the latest empirically derived equations for Md determinations are published:
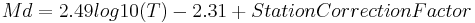( Castello et al., 2007)
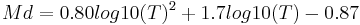( Mandal et al., 2004)
ML from Md
Although conversions between empirically derived "sensitive" seismic parameters such as earthquake magnitude scales is mathematically cautioned as well as physically limited, some seismologists such as Brumbaugh[7] have nevertheless attempted to produce a relationship linking ML to Md for a rather small sample of 17 events in Arizona:
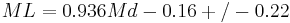
References
- ^ Bisztricsany, E. A., 1958, A new method for the determination of the magnitude of earthquakes. Geofiz. Kozl., 69-76.
- ^ Solov’ev, S. L., Seismicity of Sakalin. Bull. Earth Res. Inst.,Tokyo Univ., 1965, 43, 95–102.
- ^ Lee, W. H. K., Bennet, R. E. and Meaghu, K. L., A method of estimating magnitude of local earthquakes from signal duration. U.S. Geological Survey Open File Report, 1972, 28 pp.
- ^ Mandal, P., Narasaiah, R., Raju P. S., & R. K. Chandha, 2004. Coda duration magnitude scale of 2001 Bhuj aftershoks, India. Current Science, Vol. 87, No. 4, 2004. (India).
- ^ Castello, B., Olivieri, M. & G. Selvaggi, 2007. Local and duration magnitude determination for the Italian earthquake catalog, 1981-2002.
- ^ Mandal et al. 2004 (op. cit.)
- ^ Brumbaugh, D. S., 1989. A comparison of duration magnitude to local magnitude for seismic events recorded in northern Arizona. Jour. Arizona-Nevada Acad. Sci., Vol. 23, 29-31